| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- nvidia-smi
- 인공지능
- 머신러닝
- aof
- pandas
- ML
- selenium
- cuda
- category_encoders
- 트러블슈팅
- 그리디
- nvidia
- PYTHON
- Django
- EarlyStopping
- json
- 이것이 코딩 테스트다
- IOPub
- beautifulsoup
- Trouble shooting
- nvcc
- 잡담
- 파일입출력
- semi-project
- auc
- AI
- SMTP
- 크롤링
- Roc curve
- Logistic linear
Archives
- Today
- Total
개발 블로그
Linear Regression(선형 회귀) & Gradient Descent Algorithm(경사하강법) 본문

01 Linear Regression (선형 회귀)
종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수)x 사이의 선형 상관 관계를 모델링하는 회귀분석 기법
: 정답이 있는 데이터의 추세를 잘 설명하는 선형 함수를 찾아 x에 대한 y를 예측
(선형 회귀 : https://wikidocs.net/21670)
(선형 회귀wiki : https://ko.wikipedia.org/wiki/선형_회귀)
- 1개의 독립변수(x)가 1개의 종속변수(y)에 영향을 미칠 때 : 단순 회귀분석(Simple Regression Analysis)
- 2개 이상의 독립변수(x)가 1개의 종속변수(y)에 영향을 미칠 때 : 다중 회귀분석(Multivariate Regression Analysis)
-> 가장 적합한 θ(theta)들의 set을 찾는 것이 목표
02 Cost/Loss/Error/Objective Function (비용/손실/오차/목적 함수)
: 예측 값과 실제 값의 차이를 기반으로 모델의 성능(정확도)을 판단하기 위한 함수
Linear regression의 경우 Mean squared error function(평균 제곱 오차 함수)을 활용
-> MSE(Cost)가 최소가 되도록 하는 θ(parameter, a&b)를 찾아야 한다. (y=ax+b)
- HOW -> 경사하강법을 통해 찾는다.
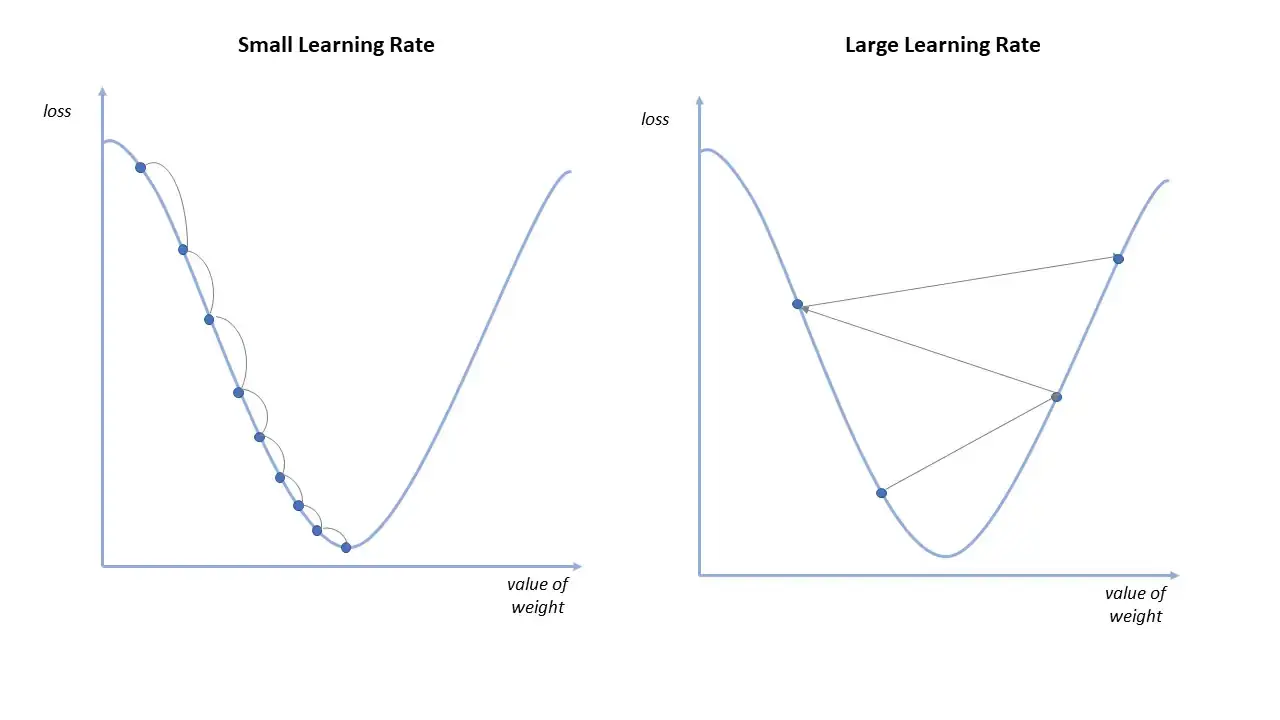
02_01 Gradient Descent Algorithm(경사하강법)
- Cost function의 값을 최소로 만드는 θ를 찾아나가는 방법
- Cost function의 Gradient에 상수를 곱한 값을 빼서 θ를 조정
-> Cost function에서 경사가 아래로 되어있는 방향으로 내려가서 Cost가 최소가 되는 지점을 찾는다.
어느 방향으로 θ를 움직이면 Cost값이 작아지는지 현재 θ위치에서 Cost함수를 미분하여 판단
(IBM : https://www.ibm.com/cloud/learn/gradient-descent)
repeat until convergence{
}

'AI' 카테고리의 다른 글
| Deep Learning이란? (0) | 2022.04.27 |
|---|---|
| Logistic Regression & Cross-entropy function & ROC Curve, AUC (0) | 2022.04.24 |
| PCA ( Principal Component Analysis) (0) | 2022.04.13 |
| K-Means algorithm (0) | 2022.04.13 |
| 인공지능과 머신러닝의 개념과 분류 (0) | 2022.04.13 |




