| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 트러블슈팅
- IOPub
- SMTP
- Django
- pandas
- aof
- selenium
- 잡담
- json
- 파일입출력
- cuda
- ML
- 인공지능
- 머신러닝
- nvidia-smi
- auc
- beautifulsoup
- Roc curve
- semi-project
- Logistic linear
- nvcc
- 크롤링
- 이것이 코딩 테스트다
- 그리디
- Trouble shooting
- AI
- nvidia
- PYTHON
- EarlyStopping
- category_encoders
Archives
- Today
- Total
개발 블로그
PCA ( Principal Component Analysis) 본문

01 PCA (Principal Component Analysis ,주성분 분석)
주성분 분석은 고차원의 데이터를 저차원의 데이터로 환원시키는 기법을 말한다. 이 때 서로 연관 가능성이 있는 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간(주성분)의 표본으로 변환하기 위해 직교 변환을 사용한다. 데이터를 한개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환한다.
(출처 : https://ko.wikipedia.org/wiki/주성분_분석)
차원 축소를 통해 최소 차원의 정보로 원래 차원의 정보를 모사(approximate)하는 알고리즘
- 차원 축소(Dimension Reduction) : 고차원 벡터에서 일부 차원의 값을 모두 0으로 만들어 저차원 벡터로 줄이는 것
- 이 때, 원래의 고차원 벡터의 특성을 최대한 살리기 위해 가장 분산이 높은 방향으로
회전 변환(rotation transform)을 진행
(참고 : https://bskyvision.com/347?category=635506)
02 실습
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import decomposition
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
model = decomposition.PCA(n_components=3)
model.fit(X)
X = model.transform(X) # 모델에 맞춰서 원래 데이터를 차원이동
""" 2PCs 시각화 """
plt.scatter(X[:, 0], X[:, 1], c=iris.target)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
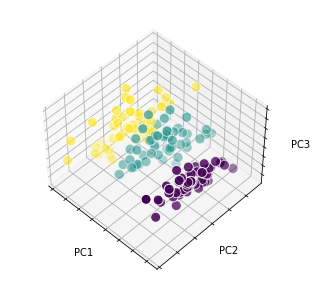
""" 3PCs 시각화"""
fig = plt.figure()
ax = Axes3D(fig, elev=48, azim=134) # Set the elevation and azimuth of the axes. (축의 고도와 방위각)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=iris.target, edgecolor='w', s=100)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
ax.dist = 12 # 값이 커지면 전체 plot 이 작아짐
plt.show()
""" 몇 개의 PC면 충분할까? """
# 각각의 새로운 축이 데이터셋의 분산(variance)을 얼마나 표현하는지 확인이 가능
print(model.explained_variance_ratio_)
# np.argmax : 최대값의 인덱스를 리턴
# np.cumsum : 누적된 합계를 계산 (cumulative sum : 누적합)
# 95% 이상의 variance 를 설명하기 위한 축의 갯수를 확인할 수 있음
print(np.argmax(np.cumsum(model.explained_variance_ratio_) >= 0.95) + 1)
# Better option (indicate the ratio of variance you wish to preserve)
model = decomposition.PCA(n_components=0.95)
model.fit(X)
X = model.transform(X)
print(X)
'AI' 카테고리의 다른 글
| Deep Learning이란? (0) | 2022.04.27 |
|---|---|
| Logistic Regression & Cross-entropy function & ROC Curve, AUC (0) | 2022.04.24 |
| Linear Regression(선형 회귀) & Gradient Descent Algorithm(경사하강법) (0) | 2022.04.15 |
| K-Means algorithm (0) | 2022.04.13 |
| 인공지능과 머신러닝의 개념과 분류 (0) | 2022.04.13 |
Comments




